Abstract
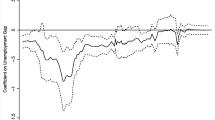
This article evaluates various models’ predictive power for U.S. inflation rate using a simulated out-of-sample forecasting framework. The starting point is the traditional unemployment Phillips curve. We show that a factor Phillips curve model is superior to the traditional Phillips curve, and its performance is comparable to other factor models. We find that a factor AR model is superior to the factor Phillips curve model, and is the best bivariate or factor model at longer horizons. Finally, we investigate a New Keynesian Phillips curve model, and find that its forecasting performance dominates all other models at the longer horizons.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Atkeson A, Ohanian L (2001) Are Phillips curves useful for forecasting inflation? Federal Reserve Bank of Minneapolis Quarterly Review 25(1): 2–11
Blinder A (1997) Is there a core of practical macroeconomics we should all believe? Am Econ Rev 87: 240–243
Calvo GA (1983) Staggered prices in a utility-maximizing framework. J Monet Econ 12(3): 383–398
Canova F (2007) G-7 inflation forecasts: random walk, Phillips curve or what else? Macro Dynamics 11: 1–30
Campbell RJ, Shiller RJ (1988) The dividend-price ratio and expectations of future dividends and discount factors. Rev Financial Stud 1(3): 195–228
Cecchetti S, Chu R, Steindel C (2000) The unreliability of inflation indicators. Current Issues in Economy and Finance. Federal Reserve Bank of New York 6(4): 1–6
Fuhrer JC, Moore GR (1995) Inflation persistence. Q J Econ 110: 127–159
Gali J, Gertler M (1999) Inflation dynamics: a structural econometric analysis. J Monet Econ 44: 195–222
Gali J, Gertler M, Lopez-Salido JD (2001) European inflation dynamics. Euro Econ Rev 45(7): 1237–1270
Gordon RJ (1982) Price inertia and ineffectiveness in the United States. J Political Econ 90: 1087–1117
Gordon RJ (1997) The time-varying NAIRU and its implication for economic policy. J Econ Persp 11: 11–32
Gordon RJ (1998) Foundations of the goldilocks economy: supply shocks and the time-varying NAIRU. Brooking Papers Econ Activity 2: 297–333
Harvey DI, Leybourne SJ, Newbold P (1998) Tests for forecast encompassing. J Bus Econ Stat 16: 254–259
King RG, Watson MW (1994) The post-war US Phillips curve: a revisionist econometric history. In: Carnegie-Rochester conference on public policy, vol 41, pp 157–219
Liu D, Jansen DW (2007) Macroeconomic forecasting using structural factor analysis. Int J Forecast 23(4): 655–677
Mishkin FS (1990) What does the term structure tell us about future inflation? J Monet Econ 25(1): 77–96
Roberts JM (2005) How well does the new Keynesian sticky-price model fits the data? Contributions Macroecon 5(1): 1206–1242
Rudd J, Whelan K (2005) Does labor’s share drive inflation? J Money Credit Banking 37: 298–312
Rudd J, Whelan K (2006) Can rational expectations sticky-price models explain inflation dynamics? Am Econ Rev 96: 301–320
Rumler F, Valderrama MT (2010) Comparing the new Keynesian Phillips curve with time eries models to forecast inflation. North Am J Econ Finan, forthcoming
Sbordone A (2002) Prices and unit labor costs: a new test of price stickiness. J Monet Econ 49(2): 265–292
Stock JH, Watson MW (1998) Diffusion indexes. NBER working paper 6702
Stock JH, Watson MW (1999) Forecasting inflation. J Monet Econ 44: 293–335
Stock JH, Watson MW (2002) Macroeconomic forecasting using diffusion indexes. J Bus Econ Stat 20(2): 147–162
Taylor JB (1980) Aggregate dynamics and staggered contracts. J Political Econ 88(1): 1–23
Woodford M (2001) The Taylor rule and optimal monetary policy. Am Econ Rev 91: 232–237
Author information
Authors and Affiliations
Corresponding author
Electronic Supplementary Material
The Below is the Electronic Supplementary Material.
Rights and permissions
About this article
Cite this article
Liu, D., Jansen, D.W. Does a factor Phillips curve help? An evaluation of the predictive power for U.S. inflation. Empir Econ 40, 807–826 (2011). https://doi.org/10.1007/s00181-010-0352-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-010-0352-0