1 Introduction

In the past few decades, orthoferrites have received particular attention thanks to their wide range of applications [1]. Iron oxide LaFeO3 is one of the most important orthoferrites with high stability over a wide temperature range [2]. Ferrites, belonging to mixed metal oxide systems, are generally represented by ABO3, where A and B are generally divalent and trivalent atoms [3]. The depletion of conventional energy resources has multiplied the demand for smarter production and storage of energy systems. The encouraging energy storage entities are supercapacitors and lithium batteries [4, 5], which are very expensive. Ferrites are very promising because of their low cost and electrochemical properties [6]. They have already shown to be adequate in fuel cells, lithium batteries, and supercapacitors [7].

The LaFeO3 compounds substituted in A-site and B-site with the general formula of La1−xAxFeO3 and LaFe1−xBxO3 have been studied thanks to their extensive usage in applications. Due to their important physical properties, La1−xAxFe1−yMyO3−d compounds (A = Ca, Sr, Ba…, M = Mn, Ti, Cr, Co…) are used in many applications, such as toxic gas detection materials [8,9,10], oxygen dense membrane [11,12,13], oxygen sensor [14], batteries [15], solid oxide fuel cells (SOFCs) [16,17,18,19,20,21,22], and catalytic materials [23, 24]. Different elaboration methods have been used to synthesize lanthanum ferrites, such as the solid-state reaction, co-precipitation, Sol–Gel, and hydrothermal [25].

Cao et al. [26] and Phokha et al. [27] found that the introduction of a transition metal into the A- and B-sites of LaFeO3 improves their physical properties. Sun et al. [28] studied the structural and electrical properties of the nanocrystalline La1−xBaxFeO3 compounds and found that the insertion of the Ba ion into the A-site can restrain the growth of grain size and enhance the response to ethanol gas. The best response to ethanol gas was obtained for a rate equal to 0.25 mol of Ba. Other detailed dielectric studies [29] have shown that the La1−xBaxFeO3 system exhibits high dielectric permittivity.

Previous studies [30] have confirmed that the appropriate amount of substitution in site A is almost 20%. In the case of double substitutions in A-site, an amount of 10% for each inserted ion improves the physicochemical properties of substituted ferrites [31,32,33].

Benali et al. [34] studied the dielectric properties of LaCaFeO3 and they showed that the electrical conduction mechanism is governed by the small non-overlapping polaron tunnel (NSPT) model.

Ferrites, having a transition metal at the B-site, have a greater tendency to occupy more than one oxidation state which affects their chemical and physical properties. The charge hop between cations at octahedral sites is the source of electrical conduction in these ferrite systems. The presence of mixed valence cations at octahedral sites improves electrical conductivity [35]. In this paper, we investigated the AC electrical conduction mechanism of La0.67Ca0.2Ba0.13Fe1−xMnxO3. To our knowledge, no such study of this material has been reported yet. Complex impedance spectroscopy is a powerful tool to analyze the grains (intrinsic) and grain boundaries (extrinsic) contributions to the electric properties of the material.

In the present work, the La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds were synthesized via the autocombustion technique. The effect of the fuel–oxidant ratio on the combustion process and the quality of obtained products was interesting. In addition, the effects of manganese doping on the structural, microstructure, dielectric properties, and conduction mechanism of the prepared La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds were studied.

2 Experimental details

2.1 Synthesis

The reagents used in the reaction were of analytical grade. The oxidants are Lanthanum nitrate La(NO3)3·6H2O, Calcium nitrate Ca(NO3)2, Barium nitrate Ba(NO3)2, Manganese nitrate Mn(NO3)3, and Ferric nitrate Fe(NO3)3·9H2O obtained from Sigma-Aldrich, Germany. The La0.67Ca0.2Ba0.1Fe1−xMnxO3 (x = 0.0, 0.03, and 0.06) perovskite compounds were synthesized by the autocombustion method according to the following reaction equation:

$$ 0.{\text{67La}}\left( {{\text{NO}}_{{3}} } \right)_{{3}} \cdot {\text{6H}}_{{2}} {\text{O}} + 0.{\text{2Ca}}\left( {{\text{NO}}_{{3}} } \right)_{{2}} + 0.{\text{1Ba}}\left( {{\text{NO}}_{{3}} } \right)_{{2}} + \left( {{1} - x} \right){\text{Fe}}\left( {{\text{NO}}_{{3}} } \right)_{{3}} \cdot {\text{9H}}_{{2}} {\text{O }} + \, x{\text{Mn}}\left( {{\text{NO}}_{{3}} } \right)_{{3}} \to {\text{La}}_{{0.{67}}} {\text{Ca}}_{{0.{2}}} {\text{Ba}}_{{0.{1}}} {\text{Fe}}_{1 - x} {\text{Mn}}_{x} {\text{O}}_{{3}} , $$
(1)

The metal nitrates were first dissolved in distilled water at a stoichiometric ratio and stirred thoroughly at room temperature for 1 h. Then, glycine (G, C2H5NO2) obtained from SD Fine Chem. Ltd., Mumbai, was added to the mixture as a fuel agent. The amount of the used fuel was calculated on the basis of the Glycine to metal ions ratio: G/M = 1.2 (rich fuel composition), which is greater than the stoichiometric quantity required to complete the combustion process without heat exchange. The temperature of the mixture was raised to 80 °C and a viscous gel was formed and annealed at 180 °C to form a dry gel. After that, the self-combustion took place at 300 °C, which originated a black powder. The resulting pellets were sintered at 700 °C.

2.2 Characterization methods

The X-ray diffractograms of the autocombustion powders were recorded using an X-ray diffractometer (D8 ADVANCE, Bruker), equipped with a CuKα radiation source (λ = 1.5406 Å) in θ–2θ Bragg–Brentano geometry. The acquisition was in the range of 5–90°, with a step of 0.02° and an acquisition time for each step of 1 s XRD. Data were subsequently refined by the Rietveld method [36], using the FULLPROF software [37] to obtain network parameters. Scanning electron micrographs (SEM) were taken with TESCAN VEGA3 SBH microscope equipped with an EDS detector Bruker XFlagh 410M. In this way, energy-dispersive X-ray analysis (EDXA) was also done.

Thermal analysis was done by Differential Scanning Calorimetry (DSC) performed using a PerkinElmer STA6000 system, with a step of 10 °C/min and nitrogen flux. With this system, both sample and reference are measured simultaneously, which is an advantage. The dielectric measurements were performed in air using an impedance spectrometer. For these measurements, a Network Analyzer Agilent 4294, operating between 100 Hz and 1 MHz in the Cp–Rp configuration (capacitance in parallel with resistance), was used [38]. During the measurement, the pellet was mechanically compressed between two parallel platinum plates functioning as electrodes.

3 Results and discussion

3.1 Structural study

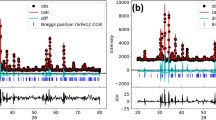
The room-temperature X-ray pattern for La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds (x = 0.00, 0.03 and 0.06) displayed in Fig. 1a revealed that all samples show the same perovskite structure. All peaks are identical and superimposable which can be assigned to the diffraction lines of the cubic LaFeO3 phase (JCPDS file COD 96-154-2145). No additional peak was observed by the substitution of the Fe3+ ions by the Mn3+ ions. All peaks are well indexed to 2θ values of 22.7°, 32.4°, 39.9°, 46.5°, 57.68°, 67.8°, 77.1°, 81.6°, 86.1°, and 95.1° indicating the 100, 110, 111, 200, 210, 211, 220, 310, 222, and 321 crystal planes, respectively. All obtained compounds crystallize in the cubic structure with the Pm\(\overline{3}\)m space group. From the XRD patterns, it can be seen that the intensity of the most intense peak [110] increased with the dopant content, which could be due to a distortion of the lattice and to a better crystallinity. Also, the patterns exhibited a slight shift of the most intense peak towards smaller 2θ values (Fig. 1b) when the Mn content increased; this indicates that Mn has a larger ionic radius than Fe. The shift of diffraction peaks toward lower angle revealed that the cell parameters of samples increase with the increase of Mn content. A typical Rietveld refinement analysis of x = 0.06 sample, using FullProf software [37], is shown in Fig. 1c. The results of the refinement of the structural parameters of our samples are reported in Table 1. A low increase in cell volume is observed when doping. The unit cell volume remains constant when x = 0.03 and 0.06. If the manganese and the iron were in a high-spin state, their ionic radii were equal to 0.645 Å, and then the volume and the lattice parameter remain invariant. The low volume increase shows that the Mn and Fe are in a low-spin state, whose ionic radii are 0.58 Å and 0.55 Å, respectively [39].

Fig. 1
figure 1

a XRD patterns for the three samples, b most intense peak of the patterns, c Rietveld refinement analysis of x = 0.06 sample pattern and d W–H plots of La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds (x = 0.00, 0.03 and 0.06)

Full size image
Table 1 Structural parameters such as, lattice constant (a), X-ray density (ρX-ray), bulk density (ρexp), porosity (P), crystallite size determined by Scherer formula (DSC) and by Williamson–Hall method (DW–H), specific surface area (S), and number of defects (δ)
Full size table

The crystallite size of all samples was determined from full width half maximum (FWHM) of the most intense peak of the X-ray spectrum, corresponding to the (110) plane using the Debye–Scherrer formula: [40]:

$$ D_{{{\text{SC}}}} = \frac{K \times \lambda }{{\beta \times \cos \theta }}, $$
(2)

where DSC is the crystal size; K is a dimensionless shape factor with a value 0.9; λ is the wavelength of CuKα1 (1.5406 Å); θ is the Bragg angle (in degrees); and β is the line broadening at half the maximum intensity (FWHM), after subtracting the instrumental line broadening, in radians. The sizes of the crystallites are approximately 44 nm, 29 nm, and 27 nm for x = 0, 0.03, and 0.06 respectively.

The Williamson–Hall (W–H) plots of the 3 compounds are shown in Fig. 1d. These plots provide a linear relationship between βcosθ and 4sinθ and the slope provides the induced strain (ε). The size of the crystallites (DW–H) is deduced from the intercept of the line with the y-axis. We notice that the straight line intercepts all the points, asserting a uniform particle size distribution of the crystallites and a very low deformation. The average size of the crystallites determined by both Williamson–Hall method and Scherer formula is reported in Table 1 for the three compounds. It is clear that the DW–H value calculated using the Williamson–Hall method is higher than the one obtained using the Scherrer equation DSC. The Williamson–Hall equation takes into consideration all diffraction peaks and assumes the broadening of it, that is related to the crystalline size as well as the lattice strain, which is not considered in the Scherrer equation [41].

The different parameters, like bulk density ρexp, X-ray density ρX-ray, and porosity P values, were calculated and are listed in Table 1. It is observed that by increasing dopant concentration the porosity (P) increases and the X-ray density (ρX-ray) is reduced. This decline in X-ray density with the substitution can be attributed to smaller weight of dopant Mn (54.938 amu) as compared to Fe (55.847 amu) [42, 43].

X-ray density (ρX-ray) was calculated taking into consideration that a basic unit cell of the cubic perovskite structure contained eight ions according to the following formula [44]:

$$ \rho_{{\text{X - ray}}} = \frac{4M}{{VN_{A} }}, $$
(3)

where 4 is the number of molecules in a unit cell of perovskite lattice, \(M\) is the molecular weight of each compound, V is the as-calculated lattice parameter converted in cm units, and \({N}_{A}\) is Avogadro’s number.

The bulk density ρexp estimated using the following relation [45]:

$$ \rho_{\exp } = \frac{m}{{\pi \cdot r^{2} \cdot h}}, $$
(4)

where \(h\), \(r,\) and \(m\) are the thickness, the radius, and the mass of pellet, respectively.

The notion of porosity has been attributed by the difference between X-ray density and the experimental density according to the following formula [46]:

$$ P\left( \% \right) = \frac{{\rho_{{\text{X - ray}}} - \rho_{\exp } }}{{\rho_{{\text{X - ray}}} }} \times 100. $$
(5)

Assuming that all the particles are spherical, the specific surface area was calculated using the following relation [47]:

$$ S = \frac{6000}{{D_{W - H} \cdot \rho_{\exp } }}, $$
(6)

where the constant 6000 is a form factor for spherical particles, DW–H is the diameter of the particle in meter (m) calculated from Williamson–Hall model, and \({\rho}_{exp}\) is the density in g/m3.

The number of defects in the sample was represented by the dislocation density (δ), which is defined as the length of the dislocation lines per unit volume of the crystal [48]:

$$ \delta = \frac{1}{{D_{W - H}^{2} }}, $$
(7)

where DW–H is the particle’s diameter in nm.

The specific surface area and the porosity of the cell units show that the distribution is almost homogeneous, and the grains are agglomerated over the entire surface of the sample. The large surface area of perovskite nanoparticles may be required for the detection and application of gas sensors [49].

To validate the existence of the cubic structure of our samples, the Goldschmidt tolerance factor is calculated [50], by the following formula:

$$ t_{G} = \frac{{\langle r_{A} \rangle + r_{O} }}{{\sqrt 2 \left( {\langle r_{B} \rangle + r_{O} } \right)}}, $$
(8)

where \(\left\langle {r_{A} } \right\rangle\)is the average ionic radius of A-site, \(\left\langle {r_{B} } \right\rangle\)is the average ionic radius of B-site, and rO is the ionic radius of oxygen [39]

The calculated value of tG was found to be 1.01 for the 3 samples, which confirms their cubic structures.

3.2 Thermal analysis

Differential Scanning Calorimetry (DSC) was done to evaluate the thermal properties of the samples. Figure 2a shows the heat flow in function of temperature for the three samples. In Fig. 2b the specific heat capacity is plotted against temperature. Specific heat capacity (Cp) was determined by the equation:

$$ C_{p} = \, \Phi /\left( {m\beta } \right), $$
(9)
Fig. 2
figure 2

a Heat flow Φ in function of temperature and b specific heat capacity (Cp) vs. temperature, of La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds (x = 0.00, 0.03, and 0.06)

Full size image

where Φ is the heat flow, m is the mass of the sample, and β is the heating rate (10 °C/min).

In the case of LaFeO3 perovskites, the minimum of the heat flow/heat capacity is considered the Neel temperature (TN) [51]. TN is 400 °C for LaFeO3 [52, 53] and after that temperature the heat flow/Cp increases sharply, because some of the energy is used in helping the random motions of the atoms during the transition. From Fig. 2a one can deduce TN of about 380 °C, 300 °C, and 330 °C for x = 0, 0.03, and 0.06 samples, respectively. Thus, the Mn doping decreases the TN, but the lower value is obtained for x = 0.03.

In what concerns Cp, the value at RT for LaFeO3 is 6.6 J/(g °C) [54]. In our case, we obtained 16.03, 9.47, and 7.92 J/(g °C) for x = 0, x = 0.03, and x = 0.06 samples, respectively. Our samples have higher Cp than the pristine LaFeO3, may be due to the existence of distortions in our samples when doping with other elements. The Mn doping approaches Cp values to the pure LaFeO3 value.

Comparing the doped samples 0.03 and 0.06, the increase of heat/specific heat above TN is not so sharp in the case of the 0.03 sample. This can be due to a slight increase in porosity (see Table 1) in this sample, which increases the disorder in the sample. We can also see in Fig. 3 that the undoped sample is more compact.

Fig. 3
figure 3

SEM images and EDS analysis of La0.67Ca0.2Ba0.13Fe1−xMnxO3compounds; a x = 0.00, b x = 0.03, and c x = 0.06

Full size image

3.3 Morphological study

Scanning electron microscopy (SEM) analysis was performed on the three compounds in order to study the surface morphology of these materials. The SEM images of the compounds La0.67Ca0.2Ba0.13Fe1−xMnxO3 (x = 0.00, 0.03 and 0.06), in Fig. 3a, show a microstructure with an almost homogeneous granular distribution. The grains are agglomerated over the entire surface of the sample.

As the doping rate increases, the porosity of the grains increases, as shown in Table 1, the morphology changes with doping. One can observe that the undoped sample is more compact in what concerns agglomeration.

The elemental analysis EDS (Energy Dispersion Spectroscopy) allows a qualitative and quantitative analysis of the elements present in the synthesized compounds. The spectra obtained (Fig. 3-EDS) reveal the presence of all the elements (La, Ca, Ba, Fe, Mn, and O) initially introduced during the preparation and that no element is volatile at 700 °C.

Nominal atomic percentages obtained by EDS associated with each element are given in Table 2. It should be noted that the compositions of the experimental samples are similar to the theoretical compositions (Table 2). Likewise, we can observe that the percentage of manganese (Mn) increases monotonically with the increase in the rate of substitution in accordance with what has been desired.

Table 2 Theoretical and experimental nominal atomic percentages obtained by EDS of the elements La, Ca, Pb, Fe, and Mn of the compounds La0.67Ca0.2Ba0.13Fe1−xMnxO3 (x = 0.00, 0. 03, and 0.06)
Full size table

3.4 Impedance studies

Impedance spectroscopy is well known as a powerful technique for studying the relaxation processes as well as the conduction mechanism of materials. This technique is widely used to quantify the contributions that constitute these materials as well as their effects on the electrical and dielectric properties. The impedance plots of the ferrites can have one or more semicircles. Usually, in ferrites, grain boundaries are highly resistive due to the presence of a higher density of structural and chemical defects compared to grain interiors. Therefore, at high frequency, the appearance of a smaller diameter semicircle is attributed to grain interiors and larger diameter semicircle is attributed to grain boundaries [55, 56].

The variation of the real part of the impedance (Z′), as a function of frequency with temperatures ranging from 160 to 360 K, is shown in Fig. 4. The behavior of Z′ observed in our samples shows three distinct regions in which changes are clearly visible with the change in temperature and frequency:

  • At lower frequencies, in region (R-1), Z′ was found to depend only on temperature; for one measuring temperature and for all compounds, the values of Z′ are constant when rising the frequency (inset Fig. 4). This could be explained by the accumulation of charge carriers at the grain boundaries.

  • In the second region (R-2), were the frequency is between about 104 and about 105 Hz (medium frequency range), the Z′ values are dependent on both frequency and temperature; they decrease when frequency increases for all compounds and also they still decrease when increasing temperature. This behavior can be related to the high mobility of charge carriers. As a consequence, this causes an increase in AC conductivity with increasing temperature and frequency.

  • At high frequencies (R-3), for frequencies higher than 105 Hz for all compounds, the real part of the complex impedance shows an independent behavior on both temperature and frequency, where all curves merge for all compounds. This behavior could possibly be related to the liberation of space charge. In fact, under the influence of temperature, a gradual reduction of charge barrier could occur [57, 58]. Thus, improving the conduction greatly reduces resistance to AC current to become negligible.

Fig. 4
figure 4

The frequency dependence of the real (Z′) part of the complex electrical impedance at different temperatures of La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds: a x = 0.00, b x = 0.03, and c x = 0.06. The insets show the three distinct regions

Full size image

Moreover, one can see at the medium frequency region (R-2) the presence of an inflexion that we will see is associated with a relaxation peak in the imaginary part of the complex impedance Z″ curves.

The variation of the imaginary part of the impedance (Z″) as a function of the frequency at different temperatures (160–360 K) is shown in Fig. 5. The values of (Z″) initially increase up to fmax then gradually decrease when the frequency and temperature increase [59]. One can see that fmax values are almost equal to the frequency values of inflexion points in Z′ curves. Furthermore, the displacement of peaks towards high frequencies with increasing temperature indicates the presence of a relaxation phenomenon in our samples (inset of Fig. 5) [60]. The presence of these Debye-type relaxation peaks indicates the existence of spatial charges as the electrical nature of spatial charges depends on the frequency [61].

Fig. 5
figure 5

The frequency dependence of the imaginary part (Z″) at several temperatures of La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds: a x = 0.00, b x = 0.03, and c x = 0.06. Insets: displacement of peaks towards high frequencies with the increasing temperature

Full size image

At high temperatures, there is a single relaxation peak which shifts to a higher frequency. This means that the charge carriers are thermally activated and accumulate at the grain boundaries. This also confirms the semiconductor nature of ferrites [62]. It is also noted that the peaks broaden with the increase in temperature, which indicates the appearance of a phenomenon of dielectric relaxation depending on the temperature.

Nyquist plots as a function of the frequency at different temperatures (160–360 K), of La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds (x = 0.00, 0.03 and 0.06), are shown in Fig. 6. The Cole–Cole plots are characterized by the appearance of semicircles where the diameter decreases with the increasing temperature. The diameter of the semi-circle is related to the resistance of the compound. The increase in temperature reduces the diameter of the semicircle, indicating that the conduction process is thermally activated and therefore the sample is semiconductor [63]. The presence of a single semicircular arc signifies a single relaxation phenomenon.

Fig. 6
figure 6

Nyquist plots of impedance data at several temperatures and the equivalent circuit of La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds: a x = 0.00, b x = 0.03, and c x = 0.06

Full size image

The Cole–Cole plots are adjusted using Z-view software [64] with combinations of equivalent circuit models presented in Fig. 6. The best fit is achieved by using an equivalent circuit, consisting of a series combination of three circuits: electrode (Re–Ce), grain boundaries (Rgb–CPEgb), and grain (Rg–Cg), where R is the resistance and CPE is the constant phase element referring to the complex element [65].

The appearance of a single semicircle is attributed to the effect of grain boundaries. It can be seen that the plots pass through the origin, which moreover excludes the existence of a possible electrode effect. The presence of the third relaxation phenomenon (third circuit) in the Nyquist impedance plots could be attributed to the inhomogeneous distribution of oxygen. In fact, during sintering, oxygen could penetrate materials through external surfaces and move through pores and grain boundaries to occupy interstitial sites.

The values of all fitted parameters are presented in Table 3. We notice that the values of Rgb are larger than those of Rg, which could be due to a disorder of the atomic arrangement near the region of the grain boundaries, thus causing an increase in the diffusion of the electrons.

Table 3 Values of electrical parameters deduced from the complex diagram at selected temperatures of La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds: (a) x = 0.00, (b) x = 0.03, and (c) x = 0.06
Full size table

The activation energy can be deduced using the Arrhenius law:

$$ R_{g,gb} = R_{0} e^{{ - \frac{{E_{a} }}{{k_{B} T}}}} , $$
(10)

where R0 represents the pre-exponential constant or characteristic resistance, kB is the Boltzmann constant, and Ea is the activation energy.

The logarithmic variation of Re, Rgb, and Rg as a function of the inverse of the temperature is shown in Fig. 7. The value of the activation energy of the grain boundaries is greater than that of the grains, which indicates a higher resistive behavior than that of the grains.

Fig. 7
figure 7

The Arrhenius plots showing the dependence resistances of grain boundaries (Rgb) and grains (Rg) versus 1000/T of La0.67Ca0.2Ba0.13Fe1−xMnxO3compounds: a x = 0.00, b x = 0.03, and c x = 0.06

Full size image

3.5 Conductivity studies

Electrical conductivity is one of the most typical assessment tools relating the behavior of charge carriers on a macroscopic and microscopic scale. To understand electrical behavior, and determine the nature of conduction and the parameters controlling this process, we have represented in Fig. 8 the variation of the ac conductivity as a function of the frequency in the temperature range 200–360 K. We noticed that there are two regions:

  • At low frequencies, conductivity increases with temperature independent of frequency.

  • At high frequencies, it is the dispersion region corresponding to the alternating conductivity, which increases with the increasing temperature.

Fig. 8
figure 8

Frequency dependency of conductivity for La0.67Ca0.2Ba0.13Fe1−xMnxO3compounds: a x = 0.00, b x = 0.03, and c x = 0.06

Full size image

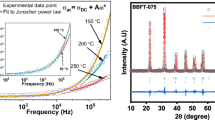
The frequency dependence of the conductivity can be expressed according to Jonscher's power law, by [66, 67]

$$ \sigma (\omega ) \, = \sigma_{{{\text{dc}}}} + \sigma_{{{\text{ac}}}} = \sigma_{{{\text{dc}}}} + \, A\omega^{S} . $$
(11)

In this expression, σdc and σac describes the conductivity in continuous and alternative currents, respectively. A is a constant depending on temperature. The exponent “S,” which represents the degree of interaction between ions and their surroundings, represents an imperative source of information about the model for the conduction mechanism in the material.

The temperature dependence of dc conductivity at f = 103 Hz is presented in Fig. 9. In this figure we can see two different regions as a function of temperature. In the low-temperature range (T < 250 K), a temperature-independent behavior is detected for all compounds. In the higher region, the conductivity increases with the increase of temperature.

Fig. 9
figure 9

Temperature dependence of dc conductivity at f = 103 Hz for a x = 0.0, b x = 0.03, and c x = 0.06

Full size image

The logarithmic variation of dc conductivity as a function of the inverse of temperature is shown in Fig. 10. This variation can be described by the Arrhenius equation as [68]

$$ \sigma_{dc} \cdot T = \sigma_{0} e^{{ - \frac{{E_{a} }}{{k_{B} T}}}} , $$
(12)

where σ0 signifies the pre-exponential factor, kB is Boltzmann constant, and Ea is the activation energy.

Fig. 10
figure 10

Variation of the Lnσdc as a function 1000/T of La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds a x = 0.00, b x = 0.03, and c x = 0.06

Full size image

From the slopes of the linear fit of Ln(σac·T) as a function of 1000/T, we can estimate the values of the activation energies associated with dc conduction. These values are found to be 0.327, 0.275, and 0.298 eV for x = 0, 0.03, and 0.06, respectively.

The ac conductivity, which obeys to the power law AωS, increases with the increasing frequency.

To determine the predominant conduction process for our compounds, we need to choose the appropriate model based on the Jonscher power law parameter "S" (Fig. 11). Based on the variation of the parameter S as a function of temperature, several models have been proposed to determine the nature of conduction, such as the Quantum Mechanical Tunneling (QMT) model where S is about 0.8 and independent of temperature [69], the Correlated Barrier Hopping (CBH) model where S decreases with the increasing temperature [70], the Non-overlapping Small Polaron Tunneling (NSPT) model where S increases with the increasing temperature [71], and the Overlapping Large Polaron Tunneling (OLPT) model where S decreases then increases with the increasing temperature [72].

  • At temperatures T < 280 K, the exponent S increases with the increasing temperature for all three compounds, the NSPT is the appropriate model to use to describe the conduction mechanism of the three compounds in this region.

S(T) can be expressed as a function of temperature by the following formula [71]:

$$ S\left( T \right) = 1 + \frac{{4k_{B} T}}{{W_{m} - k_{B} T \cdot \ln \left( {\omega \tau_{0} } \right)}}. $$
(13)

Wm represents the bonding energy of charge carriers; kB is Boltzmann's constant; and τ0 is the relaxation time.

For Wm very large compared to kBT·ln(ωτ0), the equation of S(T) becomes

$$ S\left( T \right) = 1 + \frac{{4k_{B} T}}{{W_{m} }}. $$
(14)

The values of Wm were deduced from the slope of the S(T) curves in the CBH behavior. The values are obtained in the order of 0.038 eV, 0.043, and 0.086 eV for x = 0, 0.03, and 0.06, respectively. The insertion of manganese in place of iron has an effect on the bonding energy.

  • At T > 280 K,

Fig. 11
figure 11

Temperature dependence of the exponent S of La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds a x = 0.00, b x = 0.03, and c x = 0.06

Full size image

- For x = 0, the evolution of S as a function of temperature indicates that the CBH is the very excellent theoretical model for describing the mechanism of electrical conduction. This model depicts the jumps of charge carriers between sites above the potential barrier separating them.

In this model, S(T) is given by

$$ S\left( T \right) = 1 - \frac{{6k_{B} T}}{{W_{m} - k_{B} T \cdot \left( {1 - \omega \tau_{0} } \right)}}. $$
(15)

For the large values of \(\frac{{W}_{m}}{{k}_{B}T}\), the above equation (Eq. 15) was approximated and became [73]

$$ S\left( T \right) = 1 - \frac{{6k_{B} T}}{{W_{m} }}. $$
(16)

The energy Wm, required to move an electron from one site to another, was deduced from the slope of (1 − S) as a function of temperature. It is equal to 0.086 eV. We notice the increase in the Wm value with the increase in temperature, which corresponds to the decrease in the exponent S. Thus, the number of free carriers who can jump over the barrier will increase [74].

- For x = 0.03 and 0.06.

The variation of the “S” parameter as a function of temperature suggests that the OLPT model is the most suitable model to characterize the electrical conduction mechanism in the x = 0.03 and x = 0.06 compounds, respectively. We can conclude that the substitution of Fe by Mn largely influences the conduction mechanism.

One of the fundamental characteristics of ferrites is the strong correlation between microstructure and physical properties. Our compounds have high electrical properties and good thermal and chemical stability. They are susceptible to many technological applications, such as capacitors, gas sensor, new read heads, and solid oxide fuel cells.

4 Conclusion

We have synthesized La0.67Ca0.2Ba0.13Fe1−xMnxO3 compounds (x = 0.00, 0.03, and 0.06) by the autocombustion method. Our results show that the XRD patterns of the synthesized samples present a single phase. The crystallite size value measured using Scherrer's formula was found in the range of 28 to 17 nm. The nanosize criteria were also confirmed by the Williamson–Hall method. Analysis of impedance plots in the frequency range 100 to 106 Hz and in the temperature range 160 to 360 K showed a decrease in electrical resistance. The contribution of grain boundaries is greater than that of grains. The charge carriers are thermally activated and accumulate at the grain boundaries, confirming the semiconductor nature of materials. The impedance spectra are characterized by the appearance of semicircular arcs, well modeled in terms of electrical equivalent circuit confirming the contribution of the grain and grain boundaries. The Jonscher’s power law is well fitted to the ac conductivity data. This ac conductivity analysis shows that the substitution of Fe by Mn affects the conduction mechanism model. The suitable model for all three samples is the NSPT for T < 280 K, while it is the CBH model for x = 0 and OLPT model for both samples x = 0.03 and x = 0.06 above 280 K.

The insertion of Mn in small quantities has a significant impact on the electrical properties of the compounds. This study was useful to understand the effect of Mn substitution on electrical and dielectric properties and present information for the use of these nanomaterials in high frequency devices, capacitors, and gas sensor.