1 Introduction

The prediction of slope stability is an essential task in the geotechnical engineering and other disciplines dealing, for example, with natural risk assessment. In the most cases, variations of the widely spread limit equilibrium method (LEM) are being used, calculating the total driving and resisting actions from forces and/or moments due to soil weight, surcharges, pore water pressures, anchor forces, etc. Regarding the soil resistance, shear strength in terms of friction angle \(\varphi\) and cohesion c is usually assumed using the Mohr–Coulomb criterion. The ratio of resisting to driving actions yields a numerical value of the factor of safety (FOS) which helps to interpret the state of a slope. A common LEM is the method of slices developed in several versions during the last century [2, 12, 23, 29, among others]. One disadvantage of this method is a rough approximation of the stress state along the selected slip surface as only the soil own weight and surcharges but not the stress history is considered. To overcome this aspect, approaches combining the finite element method (FEM) for calculating stresses in a soil mass with the LEM were proposed [13, 18]. A further development linking the FEM with slope stability analyses resulted in a so-called strength reduction method (SRM) [6, 10, 11, 15, 19, 20, 22, 24, 32, 33, among others]. An important feature of the SRM is a natural evolution of the critical slip surface in an arbitrary slope during the shear strength reduction [35]. Herein, a factor of safety can be determined directly from the FEM analysis independently of the LEM. However, in spite of a few attempts [27], the application of the SRM is practically limited to the perfectly plastic soil behaviour represented by friction angle and cohesion. The stress–strain behaviour of soil is neglected, and more advanced constitutive models cannot be considered in the SRM. Other advanced procedures focus on special questions like modelling of fast mass movements in partial saturated soils due to rainfalls [3,4,5] or formulate new complex numerical frameworks [7, 9].

Depending on the stress state and soil density, the stress–strain behaviour during shearing varies for loose (or soft) and dense (or stiff) soils. Whereas loose/soft soils show a gradual increase in shear stress until the critical/residual state is reached, a peak strength is observed for dense/stiff soils which then decreases to a critical/residual value in course of further shear deformation [28, among others]. A potential shear zone passes through different regions within the slope where stress and density conditions change. Consequently, the stress–strain response of the soil elements along the shear zone is not uniform.

Regarding the volumetric response, a loose/soft soil tends to a contractive behaviour during shearing. For undrained conditions, this effect is reflected in a generation of positive excess pore water pressures. On the contrary, a dense/stiff soil reveals a generation of negative excess pore water pressures during shearing in undrained conditions as the soil tends to dilate [34, among others]. Consequently, the generation of negative or positive excess pore water pressures, respectively, during shearing induces an increase or decrease in the effective stresses at the shear zone and therefore influences the soil resistance needed for the calculation of the slope stability. Within the shear zone of a slope, contractancy and dilatancy, respectively, can coexist as a result of, for example, initial stress or loading history.

In the following, a numerical algorithm is proposed for the calculation of the factor of safety taking into account a genuine stress–strain soil behaviour. Using the FEM for the slope area, realistic initial stresses within the slope can be obtained. Considering a particular deformation mechanism within the shear zone, a link between the shear strains in a slip surface and the evolution of the slope stability can be established. For the determination of such a strain-dependent slope stability, a pre-defined shear surface is discretized into nodes. The nodes can be treated as homogeneous soil elements which undergo shear deformation during the slope movement. Taking into account the soil properties, stress state, loading/deformation process and drainage conditions, numerical element shear tests with an arbitrary constitutive model can be performed. The proposed approach is illustrated by two simple calculation examples.

2 Calculation procedure

The numerical algorithm for the calculation of the strain-dependent factor of safety (FOS) consists of four basic steps:

  1. 1.

    Definition of a slip surface and its discretization

  2. 2.

    Determination of the initial stress states in the nodes along the slip surface

  3. 3.

    Numerical element test calculations within the nodes

  4. 4.

    FOS from the ratio of overall initial shear stress to mobilized shear stress as a function of shear strain

2.1 Slip surface and its discretization

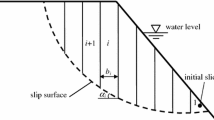
Initially, a trial slip surface has to be prescribed. Since only normal and tangential stresses within the slip surface are needed for the calculation of the FOS, there are no specific requirements on the shape of the slip surface. Nevertheless, kinematic admissible displacements of the slope should be considered, leading typically to (multi-)linear or circular slip surfaces. The trial slip surface should be varied in order to find the critical one. The search of a critical slip surface is independent of the FOS calculation. Various approaches regarding the prediction of the critical slip surface have been discussed elsewhere [8, 15, 20, among others]. Obviously, including such an approach would require a further automation of the here described procedure.

The pre-defined slip surface is discretized into a number of nodes. These nodes represent homogeneous soil elements which undergo a uniform shear deformation. Their size is immaterial as long as the applied constitutive model does not include any internal length. A certain minimum number of nodes are needed for a realistic calculation, analogously to the methods of slices.

2.2 Initial stresses

In a first approximation, the initial stresses in the nodes along the slip surface can be determined from vertical slices attributed to the nodes. Nevertheless, it is much more appropriate to generate the initial stress state within the whole slope with help of the FEM. In this way, the rotation of the principle stress axes and, eventually, a history of the slope evolution can be taken into account.

From the initial stress state in the slope, the full stress tensor is known in each node. The stress components normal and tangential to the shear zone must be evaluated from the initial stress distribution in the slope (Fig. 1). In case of a curved slip surface, its inclination varies in each node.

Fig. 1
figure 1

Step 2—determination of the normal and tangential stresses in a node on a planar slip surface

Full size image

2.3 Numerical element tests

A deformation mechanism of the sliding soil body must be assumed. In this paper, a rigid body displacement along a slip surface is considered. An example for the slope in Fig. 1 is shown in Fig. 2a. The slip surface corresponds to a shear zone undergoing a simple shear deformation. Consequently, during the slope movement each element (node) on the slip surface is subjected to the same distortion.

Fig. 2
figure 2

Step 3—the stress state on the slip surface enters the numerical routine for element test calculations (b). The static and/or kinematic boundary conditions for the element tests are selected according to the initial state and the strain state

Full size image

The rotated stress states in the nodes are supplied to a routine for numerical element test calculations (Fig. 2b). Each node represents a numerical element test reproducing the shearing in the slip surface. For the considered example of the planar slip surface, a simple shear mode is assumed. Nevertheless, other shear modes like triaxial compression or extension can be easily applied, too; see Fig. 3.

Fig. 3
figure 3

Possible deformation modes along a potential slip surface [36]

Full size image

From the numerical element tests, the shear stress evolution with increasing shear strain is obtained in all nodes; see also Fig. 2b. Depending on displacement rate, soil permeability and ground water situation, the numerical element tests can be conducted either under drained or undrained conditions. There are no restrictions regarding the applied constitutive model. The effects of excessive volumetric deformations, which may violate the prescribed kinematics of the sliding body, are being neglected.

2.4 Factor of safety

In the final step, the mobilized shear stresses as functions of shear strains are evaluated (Fig. 4). From the assumption of a rigid block displacement, in Fig. 2a, the evolution of the shear strain with the displacement is the same in all nodes. For the evaluation of the global mobilized shear resistance ratio \(T(\gamma )\), the following expression

$$\begin{aligned} T(\gamma )=\frac{\sum _i\tau _{{\mathrm{mob}},i}(\gamma )}{\sum _i\tau _{0,i}} \end{aligned}$$
(1)

is used, where \(\sum _i\tau _{{\mathrm{mob}},i}(\gamma )\) is the sum of the mobilized shear stresses of all nodes i at a certain shear strain value \(\gamma\). \(\sum _i\tau _{0,i}\) expresses the sum of the initial shear stresses in all nodes, coming, for example, from a FE calculation. As mentioned before, the orientation of the shear stresses corresponds to the inclination of the slip surface at particular nodes.

Fig. 4
figure 4

Step 4—determination of the global mobilized shear resistance ratio \(T(\gamma )\) from the ratio of the overall mobilized \(\sum _i\tau _{{\mathrm{mob}},i}(\gamma )\) to initial shear stresses \(\sum _i\tau _{0,i}\) along the slip surface as a function of the shear strain

Full size image

Equation (1) yields a global mobilized shear resistance \(T(\gamma )\) in dependence of the shear strain. In the initial state, \(T(\gamma )=1\) as \(\sum _i\tau _{{\mathrm{mob}},i}(\gamma )\) and \(\sum _i\tau _{0,i}\) are equal, whereas with shearing \(T(\gamma )\) increases, as shown in Fig. 5.

Fig. 5
figure 5

Evaluation of the global mobilized shear resistance ratio \(T(\gamma )\) during a slope displacement for soil a without and b with soil softening

Full size image

For a loose/soft soil, \(T(\gamma )\) approaches its maximum steady value when the maximum shear strength is reached in all nodes (Fig. 5a). This value can be expressed by the ratio \(\sum _i\tau _{{\mathrm{max}},i}/\sum _i\tau _{0,i}\). In case of a dense/stiff soil, \(T(\gamma )\) initially increases and further decreases with ongoing shearing (Fig. 5b). In the final state, the shear stress in all nodes is equal to the residual (or critical) shear strength. During shearing, the mobilized shear stresses \(\tau _{{\mathrm{mob}},i}\) do not reach the maximum values \(\tau _{{\mathrm{max}},i}\) simultaneously in all nodes. Consequently, the maximum of \(T(\gamma )\) is lower than the value of the ratio \(\sum \tau _{{\mathrm{max}},i}/\sum \tau _{0,i}\). In Fig. 5b, the peak of \(T(\gamma )\) represents the maximum resistance ratio which can be mobilized during the slope movement. This value is equivalent to the factor of safety for the slope taking into account the softening behaviour (Fig. 6).

Fig. 6
figure 6

Evaluation of the FOS for soil without and with soil softening

Full size image

The slope displacement, which corresponds to a particular value of the factor of safety, can be calculated from \(\gamma\) at \(T_{\mathrm{max}}(\gamma )\) considering a width of the shear zone.

It should be taken into account that the values \(T(\gamma )<T_{\mathrm{max}}\) starting from the initial state do not have any relationship to the factor of safety. However, \(T(\gamma )\) values beyond \(T_{\mathrm{max}}\) can be well interpreted as a reduction of the factor of safety with further shearing (Fig. 6). Thus, a link between the between the slope displacement and the factor of safety may be established.

3 Calculation example

The proposed procedure is illustrated by two calculation examples. In both cases a single sliding wedge on a planar weak surface, e.g. pre-existing shear surface, is considered (Fig. 7). In the first case, no softening takes place. In the second case, soil softening is included. The soil wedge is sliding as a rigid body; thus, in all nodes along the slip surface, the same shear mode and the same amount of shear strain occur.

Fig. 7
figure 7

Deformation mechanism of the sliding wedge with several selected nodes at the slip surface

Full size image

Along the slip surface, 20 nodes with the same distance between each other are defined (Fig. 7). For these nodes, the numerical element tests are conducted and the evolution of the global mobilized shear resistance \(T(\gamma )\) is evaluated during shearing; see Step 4 in Fig. 4. The number of nodes represents the number of numerical shear tests being carried out. As planar sliding of a rigid body is assumed, a simple shear mode in plain strain is considered as a representative deformation mechanism. For the calculation of the stress–strain behaviour, the linear elastic–perfectly plastic Mohr–Coulomb model is applied using the model parameters summarized in Table 1.

Table 1 Mohr–Coulomb parameters
Full size table

All calculations are performed in drained conditions; thus, the effective stresses and the total stresses are equal.

In case of the soil model without softening, after reaching the plastic state characterized by the maximum shear strength \(\tau _{{\mathrm{max}},i}\), the shear stress remains constant during further shearing. If soil softening is taken into account, the reduction rate of the friction angle from \(\varphi _{\mathrm{max}}\) to \(\varphi _{\mathrm{res}}\) is controlled by the magnitude of the plastic strain \(\varepsilon ^p_{xy}\). In the presented example, the residual value is reached for \(\Delta \varepsilon ^p_{xy}=0.2\), as shown in Fig. 8.

Fig. 8
figure 8

Reduction of the friction angle in dependence on the plastic strain \(\varepsilon ^p_{xy}\)

Full size image

Prior to the numerical element tests, a FE calculation was conducted to obtain the initial stress state in the slope by increasing gradually the gravity. For all numerical calculations, the FE software Tochnog [26] was used. The unit weight of the soil was assumed \(\gamma =20\) kN/m\(^3\). For the predefined slip surface, the stresses in the nodes along the slip surface were extracted and rotated according to Step 2; see Fig. 1.

3.1 Slope stability calculations without soil softening

The first evaluation of the strain-dependent slope stability is carried out without softening behaviour, in order to validate the numerical procedure. Each numerical soil element is distorted in shear by increasing the shear angle \(\gamma\), as shown in Fig. 10a. The induced shear strain

$$\begin{aligned} \gamma =2\cdot \varepsilon _{xy}=u/h_0 \end{aligned}$$
(2)

is linked to the thickness of the shear zone \(h_0\), the latter being a function of grain size, grain size distribution and mineralogical composition in a first approximation [1, 14, 21, 31]. u is the horizontal displacement of the shear zone boundary. In some cases, the location and thickness of the shear zone can be obtained from, for example, inclinometer tests [17, 30].

In order to prevent torsion, the upper left and right element nodes are kept at the same vertical level. A change in the soil volume takes place by a vertical displacement only.

In Fig. 9, the evolution of the normalized shear stress \(\sum \tau _{{\mathrm{mob}},i}(\gamma )/\sum \tau _{0,i}\) as a function of shear strain is shown for the nodes highlighted in Fig. 7. Due to different initial stresses along the slip surface and the \(\sigma _n\)-depended maximum shear stresses, the calculated curves differ for each considered node.

Fig. 9
figure 9

Normalized shear stress–shear strain curves during drained simple shear (for the node numbers, see Fig. 7)

Full size image
Fig. 10
figure 10

Evolution of \(\sigma _{n1}\), \(\sigma _{n2}\), \(\sigma _{n3}\) and \(\tau\) with shear strain \(\gamma\) during drained simple shear in a point 02 and b point 11

Full size image

As can be seen in Fig. 10a, in points close to the toe of the slope, e.g. point 2, the ratio of horizontal to vertical stress is greater 1 in the initial stress state (\(K_0=\sigma _h/\sigma _v=\sigma _{n2}/\sigma _{n1}>1\)) and the maximum shear stress is reached for a very small magnitude of shear strain. The shearing in plastic state is accompanied by a decrease in horizontal stress until the horizontal and vertical stresses are equal (\(K=\sigma _h/\sigma _v=\sigma _{n2}/\sigma _{n1}=1\)); see Fig. 10a. It may appear unusual that the stress–strain curves are nonlinear although the soil behaviour is characterized by the linear elastic–perfectly plastic constitutive model. This apparent nonlinearity is a result of the rotation of principal stress axes during the simple shear. The plotted components of the stress keep their orientation, whereas the principal stresses change their direction (see, for example, [25]).

The stress evolution in each node (element test) is independent of the stress evolution in its neighbourhood. This may lead to inconsistencies in the stress distribution in the soil mass during the shearing. This effect is being neglected in a first approximation.

Fig. 11
figure 11

Stress paths during drained simple shear for selected nodes along the slip surface (\(f=\frac{\sigma _1}{\sigma _3}\)). a \(\sigma _1{-}\sigma _3\)-diagram, b \(\tau {-}\sigma _{n1}\)-diagram

Full size image

During shearing, increasing shear stresses can be observed until the stress path encounters the yield surface; see Fig. 11a for principal stresses \(\sigma _1\) and \(\sigma _3\) and Fig. 11b for \(\tau\) and \(\sigma _n\). With further shearing, the stress path in the principal stresses moves downwards or upwards along the yield surface.

For nodes in the upper part of the slip surface, e.g. point 11, the initial ratio of horizontal to vertical stress is lower 1 (\(K_0=\sigma _h/\sigma _v=\sigma _{n2}/\sigma _{n1}<1\)) (Fig. 10b). In the elastic range, the shear stress increases and the stress–strain curve is linear until the stress path reaches the yield surface (Fig. 11a). For further shearing, the stress path in principal stresses moves upwards along the yield surface and the horizontal stress increases, too. Finally, the horizontal and vertical stresses become identical and \(K=1\). Meanwhile, the stress–strain curve in \(\tau\) and \(\gamma\) components increases nonlinearly until the maximum shear stress is reached (Fig. 10b).

For all the defined nodes (Fig. 7), the evolution of the global mobilized shear resistance \(\sum \tau _{{\mathrm{mob}},i}(\gamma )/\sum \tau _{0,i}\) is shown in Fig. 12. The maximum shear resistance \(T(\gamma )=\sum \tau _{{\mathrm{max}},i}/\sum \tau _{0,i}\approx 2.35\) is almost reached at the shear strain magnitude of \(\gamma \!\approx 0.6\). Thus, a maximum global shear stress 2.35 times higher than the initial global shear stress \(\sum \tau _{0,i}\) can be mobilized during the slope movement. This shear stress ratio corresponds to the factor of safety.

Fig. 12
figure 12

Evolution of the ratio of mobilized to initial shear stresses along the slip surface in dependence on shear strain

Full size image

Checking the force equilibrium of a rigid body for the given slope geometry and friction angle \(\varphi _{\mathrm{max}}= 30^\circ\), a safety factor FOS = \(\tan \varphi _{\mathrm{max}}/\tan \vartheta =2.72\) is obtained. A difference in both results can be easily explained if the Mohr–Coulomb failure criterion for simple shear is taken into account. This can be written as

$$\begin{aligned} \left( \frac{\tau }{\sigma _{yy}}\right) _{\mathrm{max}}=\left( \frac{\tau }{\sigma _{n1}}\right) _{\mathrm{max}} =\frac{\sin \varphi \cdot \cos \psi }{1-\sin \varphi \cdot \sin \psi } \end{aligned}$$
(3)

which corresponds to \((\tau /\sigma _{n1})_{\mathrm{max}}=\sin \varphi _{\mathrm{max}}=0.5\) for \(\psi =0^\circ\), see, for example, [25]. Hence, the limit stress condition in the \(\tau {-}\sigma _{n1}\)-plane has a slope \(m=0.5\) (Fig. 11b). The corresponding safety factor from the analytical solution is FOS\(\,=\sin \varphi _{\mathrm{max}}/\tan \vartheta =2.35\), i.e. identical with the numerical procedure. If associated flow rule is considered, i.e. \(\psi =\varphi _{\mathrm{max}}=30^\circ\), the limit stress condition after Eq. (3) corresponds to \((\tau /\sigma _{n1})_{\mathrm{max}}=\tan 30^\circ =0.577\) and thus FOS is 2.72.

In Fig. 12, the shear strain is indicated at the red curve when the maximum shear strength is mobilized in the selected nodes. It can be seen that the mobilization proceeds progressively from the toe and the top of the slope.

3.2 Slope stability calculations with soil softening

For the stability calculations considering soil softening, a maximum friction angle \(\varphi _{\mathrm{max}}=30^\circ\) and a residual friction angle \(\varphi _{\mathrm{res}} =12.3^\circ\) were assumed. As already mentioned, \(\varphi _{\mathrm{max}}\) is reduced in dependence on the plastic strain magnitude \(\varepsilon ^p_{xy}\) (Fig. 8). Thus, considering a non-associated flow rule (\(\psi =0\)), the limit stress condition in the \(\tau {-}\sigma _{n1}\)-plane can be characterized by a slope \(m=\sin \varphi _{\mathrm{res}}=0.213\) after Eq. (3), see also Fig. 14b, which corresponds to the safety factor \(\hbox {FOS}= \sin \varphi _{\mathrm{res}}/\tan \vartheta = 1.0.\)

Figure 13 shows the stress evolution of \(\tau\), \(\sigma _{n1}\), \(\sigma _{n2}\) and \(\sigma _{n3}\) in point 11 during shearing. When the stress reaches the yield surface, in Fig. 14a, the constitutive model switches from elastic to plastic soil behaviour and the friction angle is decreased.

Fig. 13
figure 13

Evolution of \(\sigma _{n1}\), \(\sigma _{n2}\), \(\sigma _{n3}\) and \(\tau\) with shear strain \(\gamma\) during drained shearing with soil softening in point 11. The thin lines represent the behaviour without soil softening

Full size image

With further shearing, \(\tau\) increases only slightly and it starts to decrease soon. In the principal stress plane, the softening produces an increase in \(\sigma _3\) but a gradual decrease in \(\sigma _1\) (Fig. 14a). Thus, a bending of the stress path can be observed while approaching the yield surface with an inclination of \(f=(1+\sin \varphi _{\mathrm{res}})/(1+\sin \varphi _{\mathrm{res}})=1.54\). No further stress changes occur when \(\sigma _{n2}=\sigma _{n1}\), cf. Fig. 13. In the residual state \(\tau =\sigma _{n1} \cdot \sin \varphi _{\mathrm{res}}\) with \(m=0.213\) holds (Fig. 14b).

Fig. 14
figure 14

Stress paths during drained simple shear when soil softening is taken into account. a \(\sigma _1{-}\sigma _3\)-diagram, b \(\tau {-}\sigma _{n1}\)-diagram

Full size image
Fig. 15
figure 15

Evolution of a the ratio of the mobilized to initial shear stresses in dependence on shear strain and b the corresponding strain-dependent FOS for the calculation examples

Full size image

The evolution of the global shear resistance \(T(\gamma )\) is shown in Fig. 15a. Again for some selected nodes, the shear strain is indicated when the friction angle starts to decrease due to softening. In the middle of the slip surface soil softening starts at the latest; see also Fig. 16.

A peak value of the global shear resistance \(T(\gamma )\approx 1.7\), i.e. FOS = 1.7, is observed at \(\gamma \approx 0.06\). Consequently, only 1.7 times the initial shear stress can be mobilized during the slope displacement. The global shear resistance \(T(\gamma )=2.35\) from the case without softening is not reached by far. Therefore, a standard calculation of the slope stability using the maximum friction angle \(\varphi _{\mathrm{max}}\) would strongly overestimate the safety factor. At the shear strain magnitude \(\gamma \approx 0.2\), the residual shear strength is already reached in all nodes, as shown in Fig. 16, and the safety factor approaches FOS = 1.0.

Fig. 16
figure 16

Normalized shear stress–shear strain curves during drained simple shear taking into account soil softening. The thin lines represent the behaviour without soil softening

Full size image

It should be mentioned that the soil stiffness controls the evolution of the shear stress in the elastic range and therefore strongly influences the dependence between the global shear resistance (FOS) and the shear strain. The knowledge of this dependence can help in the monitoring of slopes endangered by sliding. The rate of softening together with a relationship between the shear strain and soil displacement along the shear zone can be roughly determined, for example, in direct shear tests. Thus, using the outlined numerical procedure, a state of the slope approaching its maximum resistance can be linked to the observed slope displacements.

4 Conclusions

Safety factors in slope stability calculations are mostly determined with help of the limit equilibrium methods. In reality, however, the maximum shear strength along a slip surface is not mobilized simultaneously along the entire shear zone. This makes the selection of the appropriate shear strength parameters difficult and can lead to an overestimation but also underestimation of the slope stability.

A novel procedure for the determination of the slope stability was proposed in this paper. It takes into account the stress–strain behaviour of soils, including soil softening. Along the shear zone of an arbitrary shape, a number of nodes are defined. The initial stress state in these nodes is determined, for example, from a FEM analysis of the considered slope. An essential component of the new method is element test calculations for an assumed deformation mode in the nodes. For example, numerical simple shear tests can be performed to get the stress–strain behaviour corresponding to the displacements within the shear zone. The sum of the calculated mobilized shear stresses in all nodes can be used for the definition of the global mobilized shear resistance in dependence of shear strain. The ratio between the global resistance and the global initial shear stress corresponds to the factor of safety for the analysed slope.

The outlined procedure was demonstrated by a calculation example of a slope with a rigid body failure mechanism along a planar slip surface in drained conditions. Due to the block sliding, all nodes along the slip surface experience the same displacement. The Mohr–Coulomb model with and without soil softening, respectively, was assumed for the constitutive soil behaviour. When soil softening is considered, the maximum global shear resistance is mobilized before the maximum shear stress is reached in all nodes.

The proposed procedure can utilize any (incremental) constitutive model. Soil variations and different drainage conditions along the shear zone can be taken into account. The shape of the slip surface (shear zone) is not restricted. Its critical position must be found by changing its location and geometry.

This new approach may help to interpret the slope stability when monitoring displacements at the slip surface, see also [16].